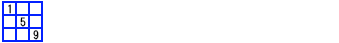トリプル数字

３つの空欄に３つの同じ候補数字

前回お伝えした「ダブル数字」は「同じエリア（タテ列・ヨコ列・９マスブロック）に２つの同じ候補数字が入っていたら、そのエリアの他のマスには同候補数字２つは入り得ない」というものでしたね。

今回お伝えする「トリプル数字」はそれとまったく同じ考え方で、同一エリアの３マスに３つの同じ候補数字が入っていたら、そのエリアの他のマスには同候補数字３つは入り得ない、というものです。
具体的に見ていきましょう。


下記画像は候補数字のメモが終わり、ある程度解き進めたものです。



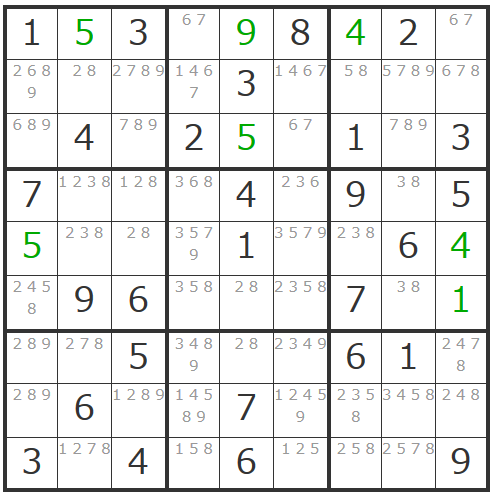
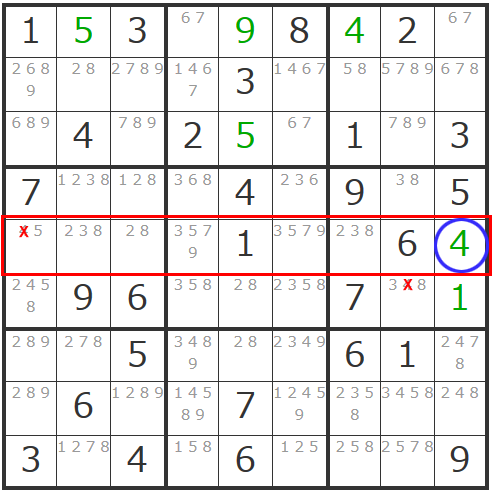
さて、中央のヨコ一列に注目してみましょう。
ここで考えるのが「２８」「２３８」「２３８」という候補数字が入った３マスです。



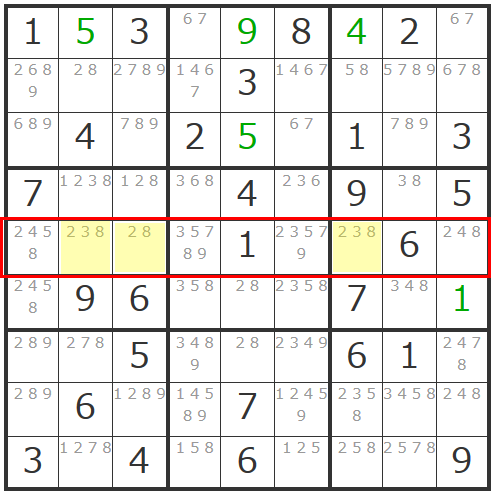
そのヨコ列では、この３マス以外にも「２」や「３」や「８」が入っていますが、仮にこの３マス以外の他のマスに「２」または「３」や「８」が確定したと考えてみてください。
例えば一番左のマスが「２」で確定したと仮定しましょう。


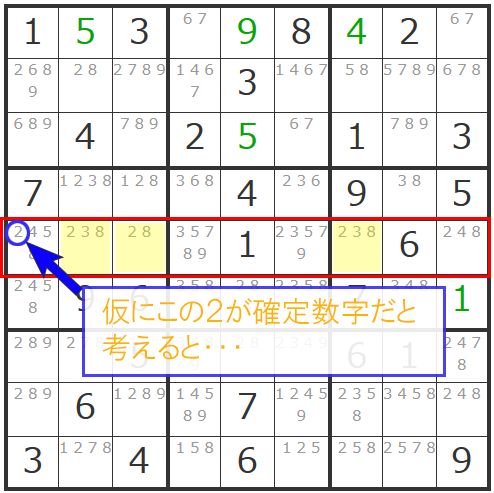
すると今回注目している３マスから「２」が消えて「８」「３８」「３８」となります。
おやおや？これでは３つのマスの候補数字が２種類（「３」と「８」）になることとなり、矛盾が発生し破綻してしまいます。


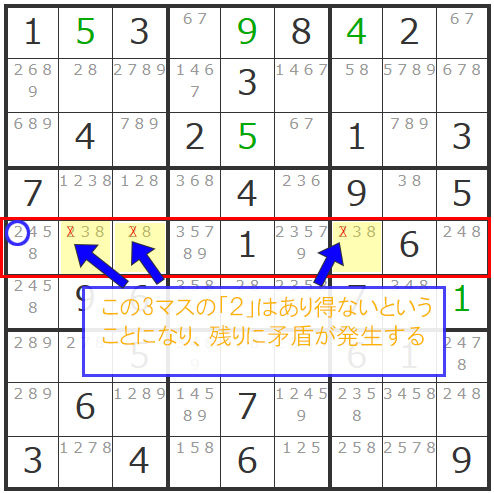
そう、今回注目した３マスのように同じエリア内の３つの空欄マスに３種類以下の候補数字しかない状態があった場合、他のマスにその数字は入り得ないのです。

逆にそのような状態になっている３マスと同じエリア内のマスにある同種の候補数字（今回の場合「２」「３」「８」）は、消すことができる、というわけです。
これが「トリプル数字」です。

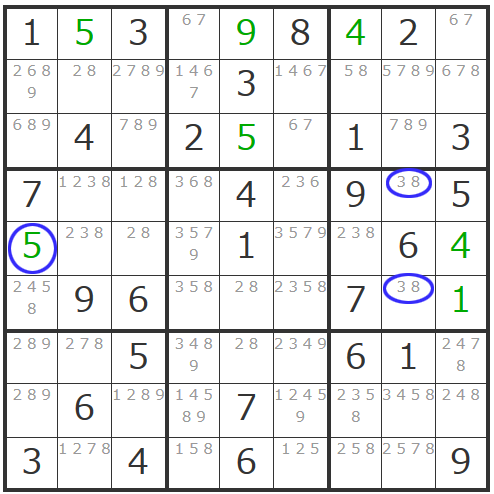
さっそく同じヨコ列の他のマスから「２」と「３」と「８」を削ってみましょう。



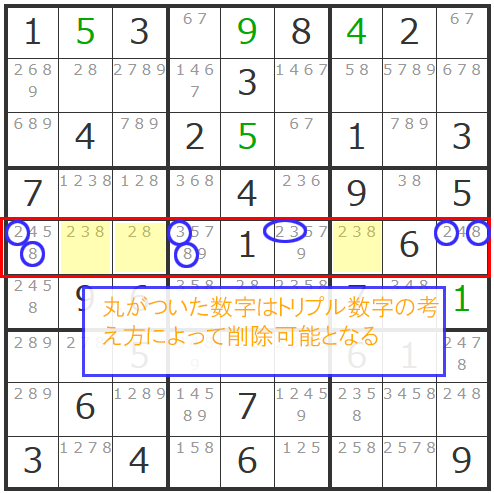
すると一番右のマスが「４」で確定できることが分かりましたので「４」で確定させましょう。


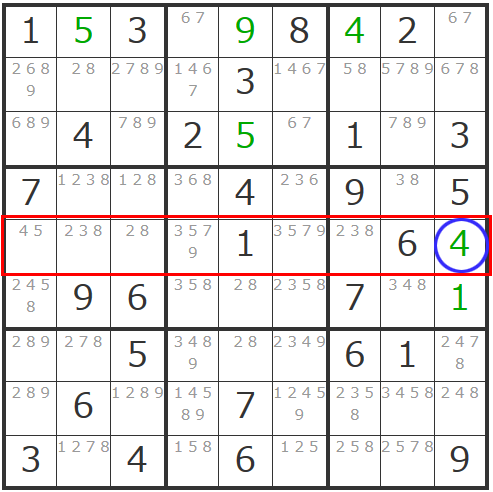
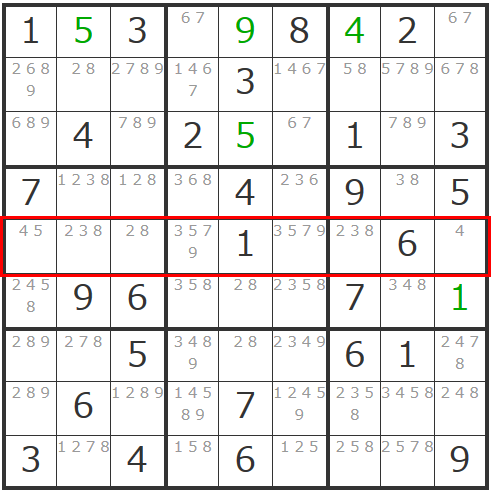
更にこの「４」の確定で影響するエリアの「４」が消えることとなり、ヨコ列の一番左のマスは「５」で確定できますし、右中央ブロックに「３８」「３８」の「ダブル数字」が現れて同ブロック内で「２」も確定することができます。




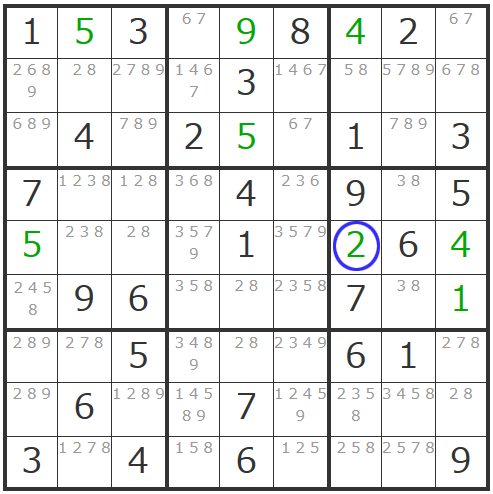
トリプル数字から離れて、この状況でもう少しいうと、先ほどの「４」の確定により、基本テクニックに立ち返って左中央ブロックの「４」も確定可能です。


「２３８」「２３８」「２３８」のような分かりやすいトリプル数字もありますが、今回例にしたように候補数字をメモする時点で１つ削れて「２８」「２３８」「２３８」のようになっていることの方が多いといえるでしょう。

また「２３」「２８」「３８」のような３つのマスの候補数字がすべて１つずつ削られているようなトリプル数字もありますので、見落とさないようにしましょう。




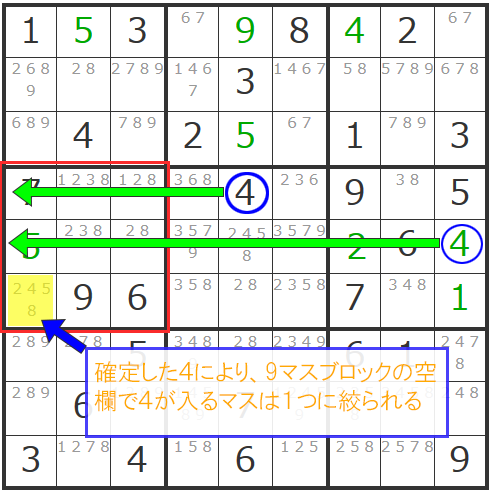
ではトレーニングとして、下の画像から「トリプル数字」を見つけてみましょう。


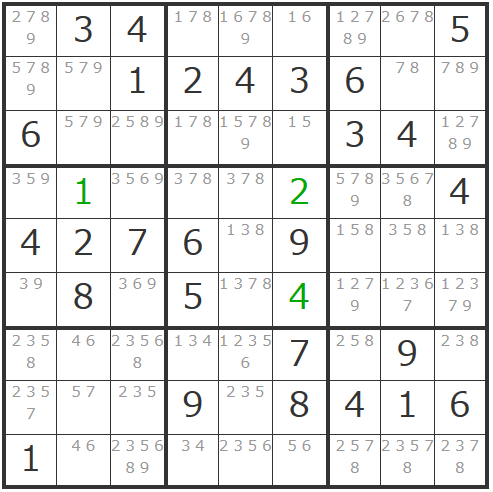
まず左上にある「５７９」「５７９」が気になりませんか？


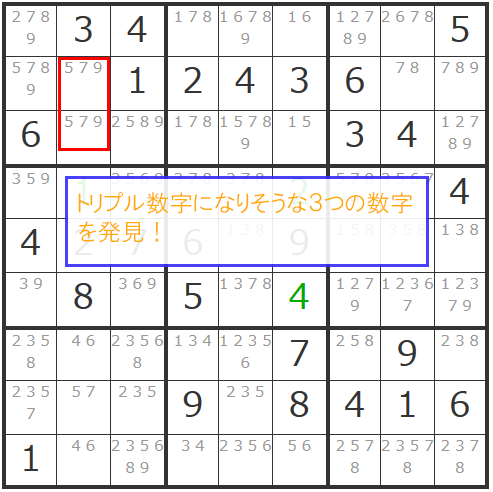
９マスブロック内には他に候補数字が３個以下のマスはないので、タテ列で追ってみましょう。
あ！あります。
下の方で「５７」を発見しました。


これで「トリプル数字」が決まり、同タテ列の他のマスから「５」「７」「９」の候補数字が消えることになります。


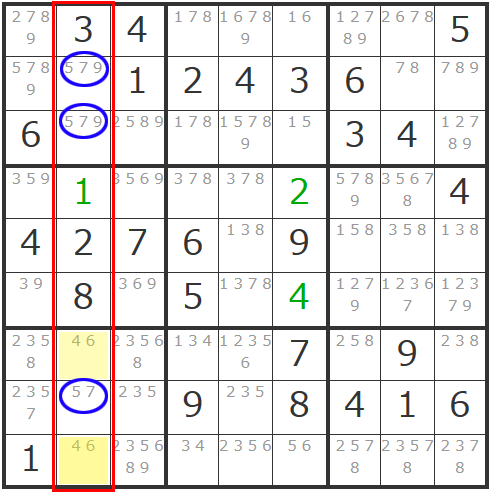
これによって新たに「４６」のダブル数字が発見されましたね！

このように２つ、あるいは３つの同じ数字の候補数字のマスがあったら「トリプル数字」がないかチェックする癖がつくと見つけやすいですよ。


トリプル数字も実際によく使うテクニックです。


次の記事
X-ウイング